О возможностях и некоторых результатах биомеханического сопровождения в челюстно-лицевой хирургии (продолжение, начало в №10(94).
А. Н. Чуйко
к. т. н., доцент (Харьков, Украина)
Д. К. Калиновский
к. м. н., Донецкий НМУ им. М. Горького (Украина)
К. Р. Пограничная
к. м. н., Львовский НМУ им. Д. Галицкого (Украина)
Р. С. Алымбаев
Киргизская ГМА (Бишкек, Кыргызстан)
2. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ИХ АНАЛИЗ
2.1. Анализ внутренних усилий в нижней челюсти в процессе откусывания пищи
В работе [2] показано, что биомеханика процессов откусывания и жевания существенно различается. Но там же показано, что изгибающие моменты у угла челюсти, наиболее опасной зоне, соизмеримы — за счет изменения плеч передачи нагрузки.
Рассмотрим оба эти процесса последовательно, используя данные CT конкретного пациента.
Ответ на этот вопрос, также как и на вопрос о прочности и жесткости НЧ после операции, является одной из целей исследования в этом разделе.
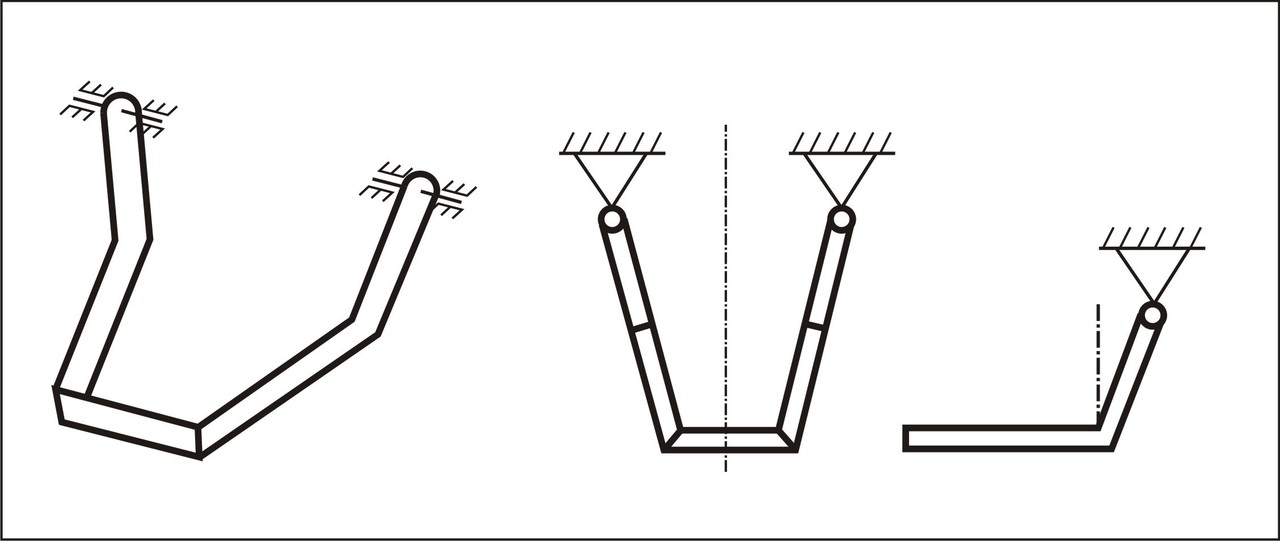
Схематизация нижней челюсти в виде пространственной рамы, представленная на рис. 10 и рис. 11, является механизмом (рис. 1), т. е. она может свободно вращаться вокруг шарниров, до возникновения какого либо ограничения. В рассматриваемом случае, ограничителем движения может являться любой зуб антагонист, который вступает в контакт с рассматриваемым зубом либо непосредственно, либо через пищевой комок.
В процессе откусывания (при включении двух передних резцов) НЧ можно представить в виде симметричной рамы с симметричным действием жевательной нагрузки, что позволяет рассматривать только половину системы. Представим нижнюю челюсть в виде плоской рамы (рис. 2). Легко увидеть, что рис. 16 повторяет рис. 10 и рис. 11, но с некоторыми дополнительными обозначениями, которые помогут в последующих рассуждениях и построениях. Особо отметим, что при такой схематизации, мы фактически предполагаем, что фронтальная часть челюсти отсутствует (рис. 1), т. е. усилия в этом элементе определить невозможно. К возможности преодоления этого допущения вернемся ниже.
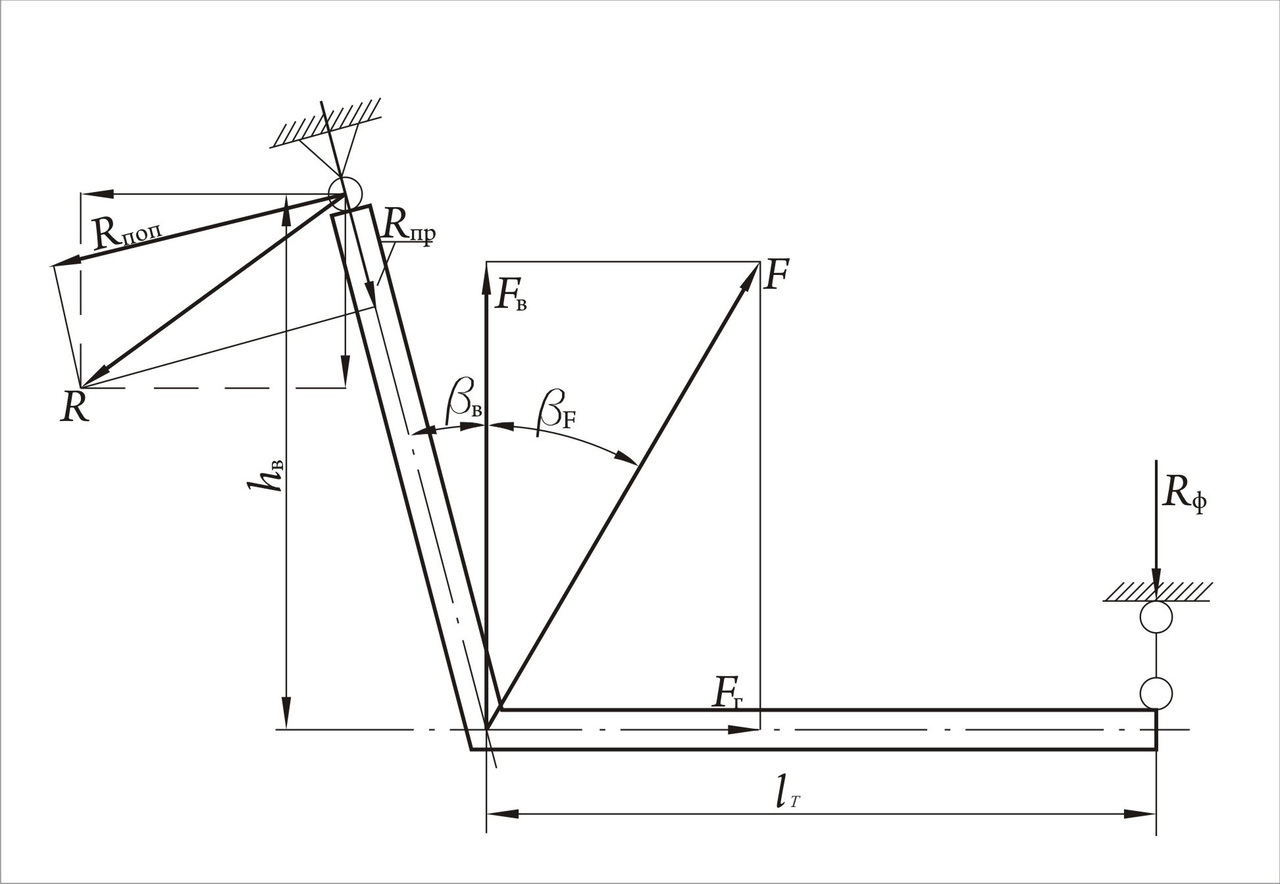
Суставная головка челюсти является классическим шарниром, как по строению, так и по особенностям функционирования. До контакта с зубом-антагонистом нижняя челюсть может рассматриваться как простейший рычажный механизм. При наличии ограничения движения в зоне резцов это плоская статически определимая рама, шарнирно опертая в двух точках (в зоне суставной головки и в зоне резцов), что схематически отражено на рис. 16 в виде неподвижного и подвижного шарниров. Реакция, возникающая в неподвижном шарнире R, может быть представлена в виде двух составляющих (например, горизонтальной и вертикальной, либо поперечной Rпоп и продольной Rпр), а в подвижном шарнире в виде одной составляющей Rф. Формулы для определения этих величин получены и приведены в [2].
Величина реакции в суставной головке R может быть использована при анализе любых проблем, возникающих в ВНЧС.
Именно эти реакции будут вызывать продольные и поперечные внутренние силы в ветви челюсти, т. е.
N = Rnp, Q = Rnon. (2)
Максимальный изгибающий момент в угле челюсти (рис. 3) равен
M = Rф lТ. (3)
Формулы (2) и (3) позволяют получить все компоненты жевательной нагрузки, величины реакций в головке и внутренних сил в произвольном сечении челюсти при любом значении силы F и геометрических параметрах челюсти.
2.2. Анализ прочности и жесткости нижней челюсти
2.2.1. Определение внутренних усилий в нижней челюсти в процессе откусывания пищи
Следуя обозначениям и данным, приведенным на рис. 10 и рис. 11, рассмотрим челюсть (рис. 3) с геометрическими размерами lТ = 70,4 мм; lв = 50,4 мм и γ = 126,6°, что дает βв= 36,6°. Примем угол действия жевательной силы βF = 30°. Так как величина жевательной силы нам неизвестна, воспользуемся приемом, реализованным в [2]. Если величина функциональной нагрузки для резца по Rus [2] Rф = 70 Н, то при принятых линейных размерах и угле действия жевательной силы, по формуле (2.6.3) [2], ее величина F = 152 Н.
Эпюры внутренних силовых факторов N, Q и M, рассчитанных по формулам (2) и (3), представлены на рис.3.
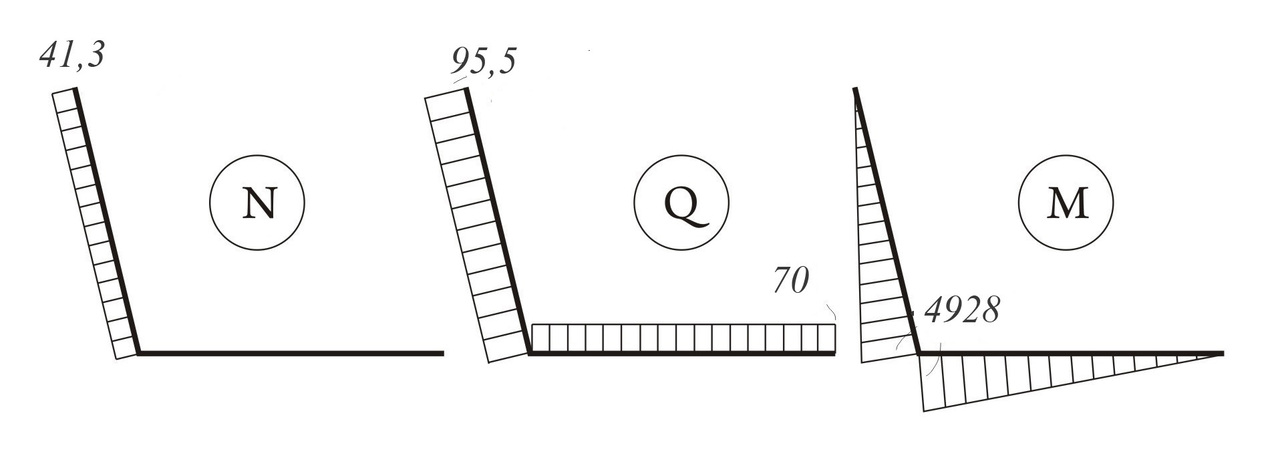
Рис. 3. Эпюры внутренних силовых факторов N (а), Q (б) и M (в). Силы N и Q указаны в Н, момент M в Нмм.
Предварительный анализ полученных эпюр показывает, что тело челюсти «работает» на сдвиг и изгиб, а ветвь челюсти — на сжатие, сдвиг и изгиб.
Таким образом, принятая расчетная схема (рис. 16) и формулы (2) — (9) позволяют получить все компоненты жевательной нагрузки, реакций в головке и внутренних сил в произвольном сечении челюсти при любом значении силы F и геометрических параметрах челюсти.
Как отмечалось выше, принятая плоская расчетная схема (рис. 2) не позволяет определить усилия во фронтальной части НЧ. Но для этого пациента, при характере его травмы, такой расчет необходим. Для решения этого вопроса рассмотрим еще одну плоскую схему, спроектировав действующие силы и реакции на фронтальную плоскость, приложив их к самоуравновешенному рычагу, опирающемуся на резцы.
Момент в поперечном сечении челюсти между резцами (в сагиттальной плоскости), из условия равновесия, можно определить по формуле
Mф = Fв by 2 — Rв bг 2 =3393 Нмм.
Нмм.
Момент в поперечном сечении челюсти в районе травмы можно определить по формуле
Mmp = Mф — Fв (by — bг 2) bг — bф bг = 2249,7 Нмм.
Нмм.
Полученные значения внутренних силовых факторов будут использованы ниже при оценке прочности и жесткости рассматриваемой челюсти.
2.2.2. Анализ уточненной расчетной схемы НЧ по данным компьютерной томографии
Напряжения и перемещения в НЧ в норме (до операции).
Для оценки прочности НЧ необходимо знать свойства костных тканей и геометрические характеристики сечений, приближенная методика расчета которых изложена в [2].
Для определения основных механических характеристик костных тканей (модуля упругости и предела прочности) в зависимости от плотности костных тканей используем эмпирические формулы (1).
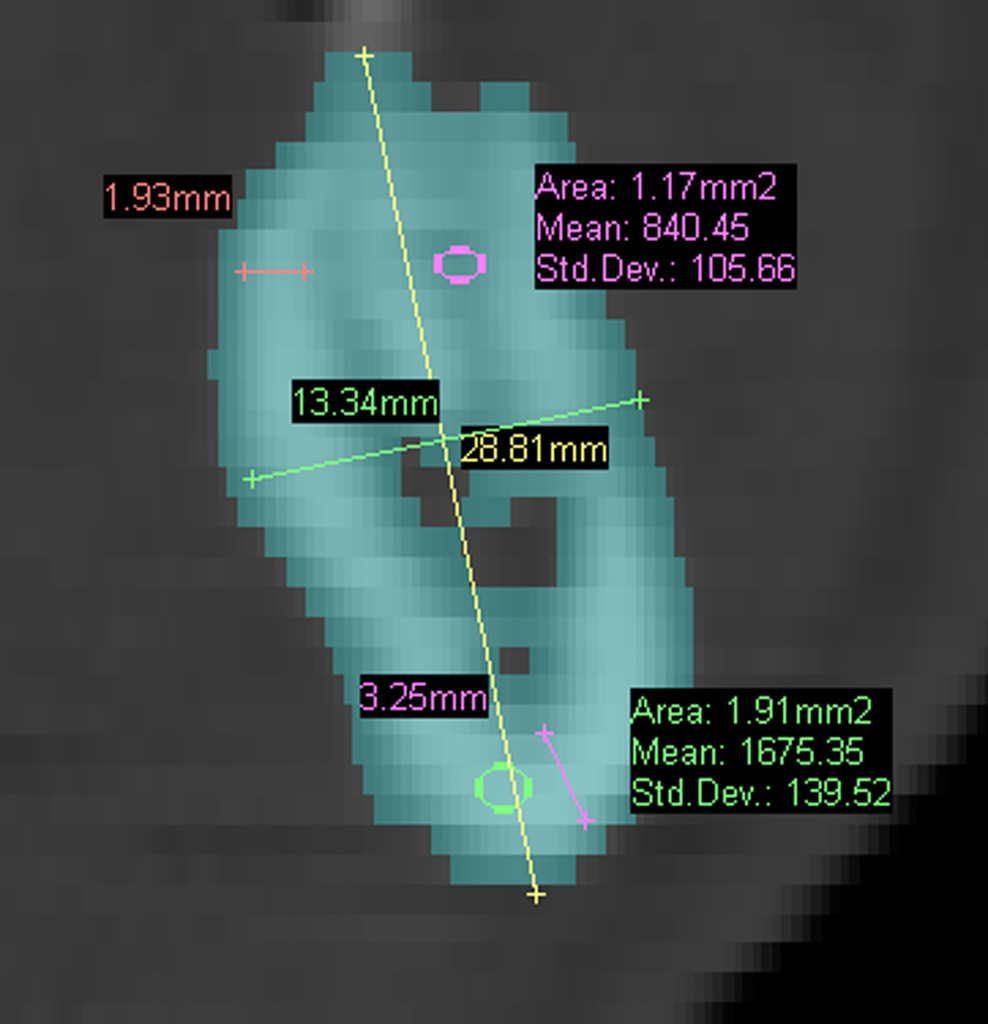
Для более точного отражения механических свойств костных тканей, рассмотрим несколько сечений НЧ в зоне отдаленной от травмы (рис. 4), результаты замеров плотности кости (HU) и линейных размеров представлены в табл. № 2.
Основные обозначения, использованные в табл. № 2, приведены на рис. 5.
Таблица № 2. Плотность кости (HU) и линейные размеры в разных сечениях
|
Параметр |
Сечение 1 |
Сечение 2 |
Сечение 3 |
Среднее значение |
|
HUк HUг |
1675 840 |
1727 345 |
1758 335 |
1720 506,7 |
|
aк bк δкн δкв aг bг |
28,81 13,34 3,25 1,93 |
24,47 14,4 3,02 1,93 |
24,69 12,66 2,89 2,13 |
26,0 13,5 3,0 2,0 21,0 9,5 |
В соответствии с данными, представленными в табл. № 2, примем средние значения чисел HU для компактной и губчатой кости соответственно HUк = 1720 и HUг =506,7. Условно совмещая начало шкалы с отметкой HU = -1024, получим ΔHUк = 2744 и ΔHUг = 1530,7. Тогда, по формулам (1) получим значения для модуля упругости и предела прочности
Ек = 42,01∙103 МПа и Ег = 7,26∙103 МПа,
σк = 429,3 МПа и σг = 133,2 МПа.
Редукционный коэффициент, который будет использован ниже, φ = 7,26/42,01 = 0,173.
Полученные значения напряжений следует трактовать как предел прочности при статическом нагружении. В то же время совершенно очевидно, что вся зубочелюстная система работает, воспринимая знакопеременные нагрузки, для оценки которых в технике (для металлов) используют предел усталостной прочности. Поскольку такие исследования для костных тканей нам неизвестны, поступим так же, как приближенно принимают для металлов, что предел усталостной прочности
σ-1 = 0,5σв = 0,5∙429,3 = 214,6 МПа.
Примем, что характерное поперечное сечение челюсти имеет форму, близкую к эллипсу (рис. 4, 5), с размерами aк = 26,0 мм; aг = 21 мм; bк = 13,5 мм и bг = 9,5 мм (рис. 5). Смещение центров тяжести эллипсов, ограничивающих компактную и губчатую кость равно yг = 0,5 мм.
Площади поперечных сечений и моментов инерции соответствующих компонентов кости по внешнему контуру определим по формулам [2], с учетом редуцирования сечений и смещением центров тяжести.
Редуцированная площадь поперечного сечения равна
A= 146,11 мм2.
Момент инерции сечения относительно поперечной центральной оси равен
J = 8,118∙103 мм4
Действующие напряжения в ветви челюсти от сжатия и сдвига определяются как
σ = N A = 41,3/146,11 = 0,283MПa;
τ = Q A=95,5/146,11 = 0,654MПa.
Действующие напряжения от изгиба определяются по формуле
σ = M J ymax = 4928∙13,44/8,118∙103 = 8,16MПa.
Сравнение численных значений напряжений от сжатия, сдвига и изгиба подтверждает принятое выше допущение о том, что напряжения от сжатия и сдвига существенно меньше напряжений от изгиба.
Если принять по данным CT, что травмирующие напряжения равны принятому значению усталостной прочности, т.е. σТ = σ-1 = 214,6 МПа, получим значение коэффициента запаса прочности
k = σТ σ = 214,6/8,16 = 26,3.
.
Таким образом, коэффициент запаса прочности нижней челюсти пациента Л в норме (до операции) при откусывании, равен 26,3. В [2] для виртуальной челюсти получено значение k = 15. Эти цифры показывают, что обычный человек при нагрузках близких к норме проблем с прочностью челюсти не испытывает, как в режиме откусывания и жевания, так и при занятиях спортом и бытовых нагрузках.
В качестве контрольной цифры можно запомнить, что в норме при откусывании пищи, коэффициент запаса прочности челюсти более 15. Такой вывод в известной нам литературе отсутствует.
После решения задачи прочности — определения действующих напряжений рассмотрим задачу жесткости — определение перемещений. Учитывая, что напряжения от сжатия и сдвига значительно меньше, чем напряжения от изгиба, при определении перемещений будем учитывать только изгиб челюсти. Используя интеграл Мора и метод моментных площадей (правило Верещагина), после несложных преобразований, для перемещений угла челюсти Δ, получим
Δ = Rф l3Т 3 EJ 1 +lв lТ. (4)
. (4)
После подстановки Rф по (2.6.3) [2], выражение для податливости δ будет иметь вид
δ = lв l2T sin(βF + βв) 3EJ lT + lв lT + bв. (5)
. (5)
Анализ формулы (5) показывает, что податливость челюсти δ, при силе приложенной к ее углу, зависит от длин тела челюсти lT и ветви челюсти lв, углов наклона жевательной силы βF и ветви челюсти βв и жесткости челюсти на изгиб EJ.
Для принятых выше параметров по формуле (5) получим
δ = 2,93∙10-4 мм/Н.
Для сравнения приведем величины податливости отдельных зубов по [2], которые лежат в диапазоне от 1,42∙10-3 мм/Н (для моляра) до 2,79∙10-3 мм/Н (для премоляра). Отметим, что жесткость самого зуба достаточно велика, а его податливость определяется наличием периодонта. Таким образом, податливость НЧ за счет ее общей упругости на порядок меньше податливости отдельных зубов в норме и может, при необходимости, учитываться, как при анализе любых перемещений в системе, так и окклюзонных соотношений зубов.
Методика определения податливости НЧ и вычисление ее значения для конкретного пациента, очевидно, излагается впервые.
Абсолютные значения перемещений Δ можно определить из соотношения
Δ = δ ∙F. (6)
Полученные значения напряжений и перемещений, характеризуют напряженно-деформированное состояние челюсти пациента Л в норме.
Общий вывод. Значения напряжений и перемещений НЧ в норме должны служить базой (отправной точкой) для исследования напряженно-деформированного состояния при любых патологических изменениях.
Напряжения и перемещения в НЧ в зоне сетчатого имплантата (после операции).
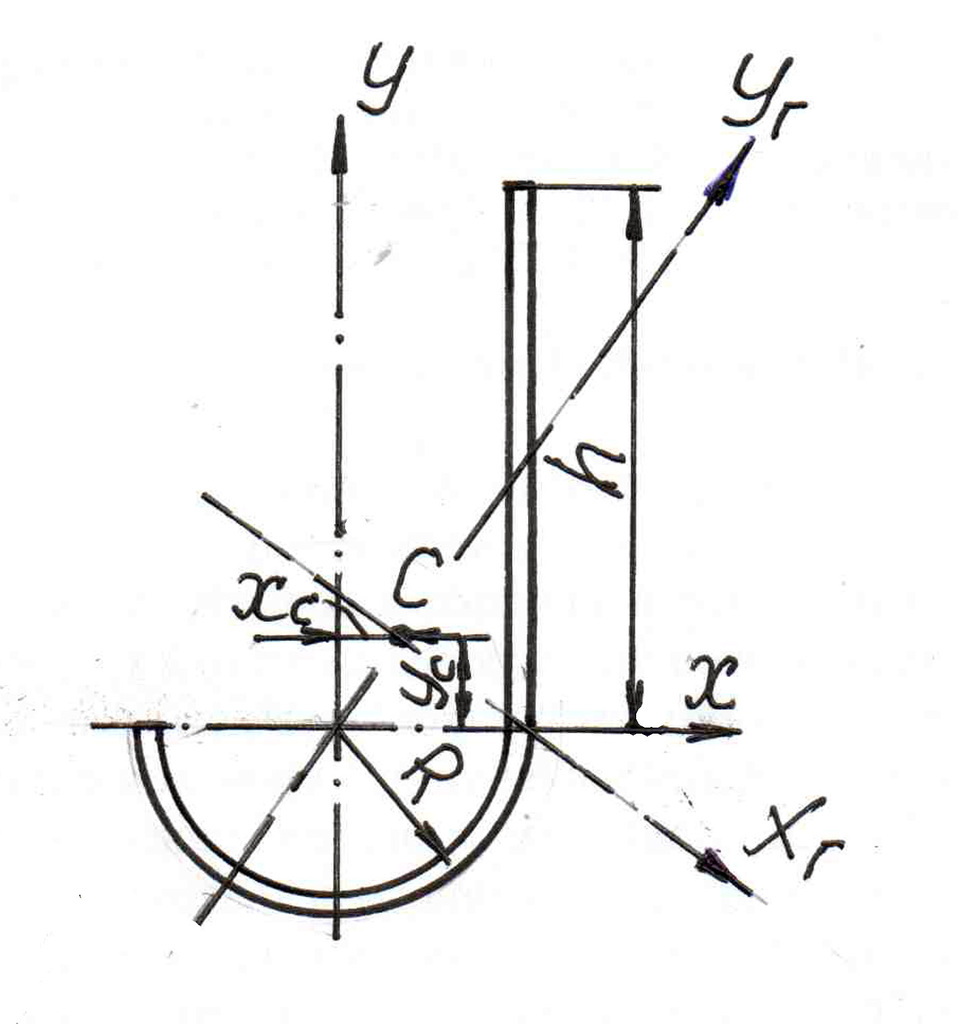
Для построения расчетной схемы НЧ после операции вначале рассмотрим геометрические характеристики сетчатого имплантата с учетом его изготовления (изгиба) и подгонки в процессе операции (рис. 1.18 [1]). На рис. 6 показаны линейные размеры СИ в зоне сагиттального сечения, а на рис. 7 расчетная схема его поперечного сечения.
Следуя размерам, приведенным на рис. 20 примем h = 15,52 мм, R = 4,61 мм, толщина пластинки δ = 0,6 мм. По формулам, использованным выше, можно, после достаточно трудоемких вычислений, определить
— положение центра тяжести сечения
xc = 0,53 мм, yc =2,6 мм;
— моменты инерции относительно центральных осей
Jx = 125,6 мм4, Jy = 15,4 мм4 и Jxy = 184 мм4;
— угол поворота главных осей
α = 36,6°
и другие механические характеристики. Подчеркнем, что при вычислении этих характеристик, принято, что коэффициент перфорации сечения к = 0,167.
Далее вычислим моменты сопротивления — геометрические характеристики, определяющие прочность сечения:
для сечения в форме эллипса (кости в норме)
Wx = Jx ymax = 6,04∙102 мм3;
мм3;
для сечения сетчатого имплантата (рис.7)
Wx = Jx ymax = 9,72 мм3.
мм3.
Таким образом, при прочих равных условиях, прочность кости в норме (до операции) выше, чем прочность СИ заданного профиля в
Wx,эWx,си = 604 9,72 = 62 раза.
раза.
Так как изгибающие моменты в угле челюсти и в зоне перелома различные, определим максимальные нормальные напряжения в СИ
σ = Mтр Wx,си = 231 МПа.
МПа.
Сравнивать эти напряжения следует с допускаемыми напряжениями для титана, из которого изготовлен СИ. Так как марка титана, из которого изготовлен СИ, неизвестна, примем, следуя [2], для титана σт = 275…450 МПа. Даже при верхнем значении этой величины, принимая
σ-1 = 0,5σT = 0,5∙450 = 225 МПа,
т.е. прочность СИ сразу после операции, до заполнения перелома костной тканью, недостаточная.
Единственная рекомендация пациенту — после операции при откусывании пищи развивать усилия меньше 70 Н, т. е. усилий при которых был проведен весь изложенный выше расчет.
При наличии в системе даже одного небольшого участка с пониженной жесткостью, в данном случае в зоне сетчатого имплантата, этот участок можно рассматривать как упругий шарнир. Определение угловых перемещений в зоне перелома можно провести по формуле
θ = M∙l EJ. (7)
. (7)
Вначале определим жесткость на изгиб сечения кости НЧ и сечения СИ, в зоне перелома, приняв для титана [2] модуль упругости E = 1,1 ∙105 МПа
(EJ)k =42,01∙103 ∙8,118∙103 = 341∙106 Нмм2;
(EJ)си =1,1∙105 ∙1,25∙102 = 137∙105 Нмм2,
т. е. жесткость кости в 25 раза выше, чем у сетчатого имплантата выбранного профиля.
Далее, учитывая, в соответствии с рис.6 и 7, что дефект в зоне перелома после операции имеет ширину порядка 5 мм, подставим все полученные значения в формулу (7)
θk = M∙l (EJ)к = 3,21∙10-5 рад или θк = 1,9∙10-3 град.
рад или θк = 1,9∙10-3 град.
θси= M∙l (EJ)си = 8,21∙10-4 рад или θси = 4,68∙10-2 град.
рад или θси = 4,68∙10-2 град.
Полученные значения углов позволяют определить взаимные линейные перемещения кромок кости в зоне перелома. В технике это носит название «раскрытие стыков». Принимая расстояния от центра тяжести сечения до максимально верхней точки сечения (в соответствии с рис. 21) yк = 13,44 мм и yси = 18,79 мм, получим
Δlк = θк ∙ yк = 3,21∙10-5∙13,44 = 4,3∙10-4 мм;
Δlси = θси ∙ yси = 8,21∙10-4 ∙ 18,79 = 1,54∙10-2 мм.
Из полученных значений взаимных перемещений кромок для клинической практики представляет интерес, в первую очередь, значение перемещений в зоне СИ. Насколько перемещения в 0,015 мм влияет на процесс восстановления кости?
Учитывая, что горизонтальная проекция расстояния от перелома до суставных головок равна lТ + bв = 70,4 + 30,05 = 100,45 мм, перемещения головок
S = (lТ + bв) θси = 100,45∙8,21∙10-4 = 8,25∙10-2 мм.
Несмотря на то, что полученные значения перемещений головок небольшие, отметим и такой факт. Из-за несимметричности сечения (рис. 6) и несовпадения силовой плоскости, в которой действует изгибающий момент, с плоскостью проходящей через главные оси координат, в рассматриваемом случае будет происходить так называемый косой изгиб, который характеризуется тем, что вектор перемещений направлен под углом
tgβ = Jx Jy tgα, (8)
, (8)
где α — угол между силовой плоскостью и плоскостью проходящей через главную ось координат.
Эта особенность упругих перемещений челюсти в зоне СИ вызовет боковые перемещения суставных головок, что может быть обследована дополнительно, особенно с учетом отзыва пациента.
Кроме того, отметим, что в соответствии с расчетной схемой (рис.11, №10 (94)) при разжевывании пищи система становится несимметричной. В этом случае, как показано в [2], жевательная нагрузка передается с одной части тела челюсти на другую за счет кручения фронтальной части НЧ. Но фронтальная часть челюсти фактически представляет собой незамкнутый контур, который плохо воспринимает нагрузку, приводящую к кручению. В [2] этим объясняется то, что в процессе эволюции фронтальная часть НЧ стала более массивной. Но этот же эффект – повышенного кручения открытого профиля, будет характерен и для рассматриваемого сетчатого имплантата. Это явление также предполагается обследовать дополнительно.
После восстановления зубных рядов (протезирования) по такой же методике может быть рассмотрен и процесс жевания, в соответствии с рекомендациями, изложенными в [2].
В заключение данного раздела отметим, что сформулированные в разделе 1.1 условие прочности или аналогичное ему условие жесткости взаимно связывают КОНСТРУКЦИЮ (ЧЕЛЮСТЬ В НОРМЕ ИЛИ ПРИ ПАТОЛОГИИ) — СВОЙСТВА КОСТНЫХ ТКАНЕЙ (КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ) – НАГРУЗКУ. Из этой триединой взаимосвязи составляющих каждого из условий выше, при рассмотрении травмы конкретного пациента, первые две — КОНСТРУКЦИЯ (ЧЕЛЮСТЬ В НОРМЕ ИЛИ ПРИ ПАТОЛОГИИ) и СВОЙСТВА КОСТНЫХ ТКАНЕЙ (КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ) рассмотрены на основе данных СТ пациента (в том числе контрольной). НАГРУЗКА рассмотрена на основе статистических данных. После разработки методики определения величины жевательной нагрузки конкретным пациентом с учетом восстановления костных тканей после операции, предлагаемая методика определения напряжений и перемещений в челюсти после операции приобретет конкретный, законченный характер.
Выводы и практические рекомендации
1. Разработанная и адаптированная в [1, 2] для челюстно-лицевой хирургии, методика реконструкции травмированной челюсти без вскрытия операционного поля, как элемента технологии CT/CAD/CAM/CAE, позволила рассмотреть задачу прочности и жесткости НЧ конкретного пациента после реконструкции.
Показана эффективность предлагаемой методики по применению современных компьютерных технологий в ЧЛХ, как при наличии первичной CT, так и после проведения контрольной CT.
2. Анализ напряжений и перемещений в нижней челюсти пациента по данным контрольной томографии через 22 дня после операции показывает, что прочность установленного сетчатого имплантата находится на нижнем пределе запаса прочности и жесткости, чем, очевидно, можно объяснить медленное восстановление ложного сустава.
3. При необходимости повторной операции можно рассмотреть: 1) конструкцию сетчатого имплантата, разработанного строго по конфигурации корректно соединенных частей челюсти; 2) несколько вариантов пластинчатых имплантатов, расположенных как на фронтальной части подбородка, так и под ним. Эффективность обоих вариантов операции может быть оценена с помощью расчетов на прочность и жесткость.
Изготовление имплантатов (их изгибание из стандартных заготовок) можно проводить по виртуальным стереолитографическим моделям.
4. Расчеты на прочность и жесткость либо по приближенной методике, либо более точно, на основе конечно-элементного моделирования и анализа, позволят ответить на вопросы о рациональности и долговечности проведенной реконструкции.
5. Для биомеханического обоснования принимаемых решений, особенно на этапе планирования операции, в бригаду должен входить специалист, владеющий основами биомеханики хотя бы в степени, достаточной для проведения необходимых расчетов.
Следует ожидать существенных изменений в уровне подготовки и характере работы черепно-челюстно-лицевых хирургов с опорой на современные компьютерные технологии.
Литература
1. Чуйко А. Н., Калиновский Д. К. О некоторых возможностях современных компьютерных технологий в челюстно-лицевой хирургии // ДенталЮг. — 2011, № 1—2. С. 49—53.
2. Чуйко А. Н., Шинчуковский И.А. Биомеханика в стоматологии: Монография. — Х.: Изд-во «Форт». 2010. — 516 с.
3. Гинали В. Н. Изменения височночелюстного сустава при потере зубов. Под ред. проф. А. Т. Бусыгина. — Т.: Медицина, 1966. 84 с.
4. Копейкин В. Н., Курляндский В. Ю., Кнубовец Я. С., Оксман И. М. Зубопротезная техника. — М.: Медицина, 1967. — 432 с., ил.
5. Гаврилов Е. И., Щербаков А. С. Ортопедическая стоматология: Учебник 3-е изд., перераб. и доп. — М.: Медицина, 1984. —576 с., ил.
6. Советский энциклопедический словарь / Гл. ред. А. М. Прохоров. — Изд. 4-е — М.: Сов. энциклопедия, 1987. — 1600 с.
7. Чуйко А. Н., Маргвелашвили А. В. О некоторых особенностях расчета нижней челюсти
при функциональной нагрузке // Российский журнал биомеханики. — 2009, № 2. — С. 69—79.
8. Чуйко А. Н., Шинчуковский И. А. Определение основных механических характеристик костных тканей на базе данных компьютерной томографии // Современная стоматология. — Киев. — 2011, № 1. — С. 90—98.
9. Lekholm U., Zarb G. Patient selection and preparation. In: Branemark, P.-I., Zarb G., Albrektsson T., eds. Tissue integrated prostheses, 117—128. Chicago: Quintessense (1985).
10. Mow C., Hayes W. C. Basic Orthopedic Biomechanics, New York 1991.