Математический анализ компьютерного моделирования адгезивных конструкций
И. К. Луцкая
д. м. н., профессор БелМАПО (Минск)
Н. А. Юдина
д. м. н., профессор, заведующая кафедрой общей стоматологии Белорусской медицинской академии последипломного образования (Минск)
Актуальной и одновременно сложной для решения задачей современной стоматологии является рациональное и полноценное восстановление целостности зубного ряда. Отсутствие группы жевательных и фронтальных зубов ряда оказывает негативное влияние на качество жизни индивида, включая как функциональный, так и эстетический аспект данной проблемы. Появление малого дефекта зубного ряда может не вызывать значительного нарушения функции откусывания или пережевывания пищи, но тем не менее, служит этиологическим фактором развития зубочелюстных аномалий и деформаций, распространенность которых составляет 28,8-55,0% от числа взрослого населения [1,2].
Разработки современных методов анализа, обоснования и прогнозирования лечения пациентов с нарушением зубных дуг требуют тесной взаимосвязи медицинских, теоретических и технологических аспектов науки. Проведение исследований по усовершенствованию замещающих конструкций предусматривает использование фундаментальных теоретических разработок в области высшей математики и вычислительной техники. Так, применение методов математического и компьютерного моделирования существенно расширяет возможности экспериментальной и клинической практики [3, 4, 5]. Теоретические выкладки позволяют обосновать пути оптимизации конструкций замещающих протезов, прогнозировать сроки их эксплуатации, функциональное состояние опорных зубов и прилежащих к ним тканей [1, 3, 7].
Для восполнения малых дефектов зубных рядов современная стоматология располагает большим арсеналом восстановительных методик. В него наряду с классическими протезами входят и достаточно новые, перспективные, динамично развивающиеся технологии. Одной из них является изготовление адгезивных конструкций на основе волоконного армирующего каркаса и композиционной облицовки. Данная малоинвазивная методика обладает рядом преимуществ, о чем свидетельствуют результаты научных исследований по данной тематике и большой интерес практикующих врачей. Дискуссионными остаются вопросы, связанные с прочностными характеристиками адгезивных волоконных конструкций, прогнозом результатов лечения в отдаленные сроки и показаниям к выбору конструкции данных протезов [2].
В опубликованных научных работах представлены ограниченные данные о влиянии расположения армирующего каркаса на показатели прочности адгезивных конструкций, что затрудняет разработку показаний дифференцированного выбора средств и методов реставрации дефектов зубного ряда [1, 6, 8].
Цель исследования
Анализ результатов компьютерного моделирования напряженно-деформированного состояния (НДС) адгезивных волоконных конструкций (АВК) в зависимости от расположения армирующего каркаса с обоснованием оптимального варианта лечения в различных условиях.
Материалы и методы исследования
Для проведения расчетного определения НДС геометрически сложной биомеханической системы «зуб-протез», которая образуется при фиксации АВК на опорных зубах, был использован численный математический анализ на основе метода конечных элементов. Объектом исследования служили разработанные математические модели, отражающие функциональные особенности и строение системы «зуб-протез», включающей естественные опорные зубы, а также искусственные зубы, коронковая часть которых воссоздана с помощью адгезивных волоконных конструкций с различными вариантами расположения армирующего каркаса.
Построение геометрических и конечно-элементных моделей, задание граничных условий, приложение нагрузок и расчет НДС АВК выполнялись в программном комплексе конечно-элементного анализа «ANSYS» (ANSYS Inc., США) на базе объединенного института машиностроения Национальной академии наук Беларуси. Поставленная задача решалась в трехмерной постановке. Рассматривались два вида нагружения моделей, отличающихся количеством и направлением действующих сил. Искомыми результатами расчета служили максимальные значения узловых растягивающих и эквивалентных (по Мизесу) напряжений, возникающих в конструкциях, а также графические материалы, отражающие картину НДС системы «зуб-протез» в виде изолиний полей напряжений для каждого режима нагружения. Результаты расчета НДС АВК являлись исходными данными для проведения сравнительного анализа напряжений материала конструкций и выявления оптимального варианта расположения армирующего каркаса.
Исследование состояло из трех этапов:
- Построение трехмерных геометрических моделей АВК с различными вариантами расположения армирующего каркаса в системе «зуб-протез».
- Разработка конечно-элементных моделей АВК с различными вариантами расположения армирующего каркаса и задание граничных условий для расчета.
- Расчет НДС АВК с различными вариантами расположения армирующего каркаса и анализ полученных результатов.
При разработке математической конечно-элементной модели АВК в системе «зуб-протез» были приняты следующие допущения: материалы компонентов модели считаются изотропными, а для описания их свойств достаточно таких механических характеристик как модуль Юнга и коэффициент Пуассона, то есть нелинейные свойства материалов не учитываются. Исследования проводятся только в линейной области.
В качестве исходных данных для построения моделей и их численной обработки была использована следующая информация: морфометрические параметры зубов и прилежащих к ним тканей; классическая методика изготовления адгезивных волоконных конструкций; механические характеристики зубных и прилежащих к ним тканей, светоотверждаемого композиционного материала и армирующей волоконной системы.
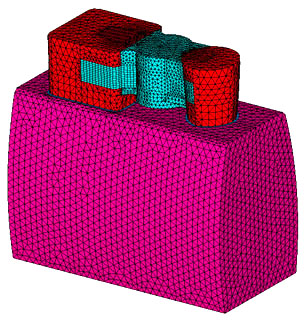
На первом этапе, на основании морфометрических параметров зубов и прилежащих к ним тканей проводилось построение объемных геометрических моделей АВК в системе «зуб-протез». Геометрические модели разработаны на основе строения клинических моделей АВК, для создания которых был определен вариант отсутствия второго премоляра, с двухсторонней фиксацией протезов на опорных зубах: мезиально – на первом премоляре, дистально – на первом моляре (рис. 1).
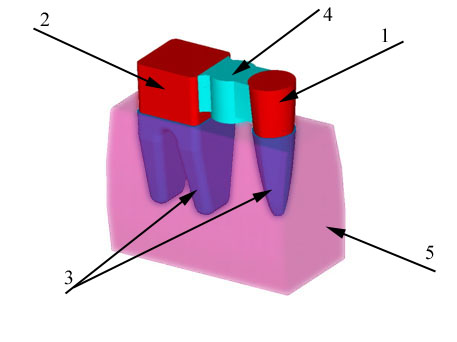
Рис. 1. Общий вид трехмерной геометрической модели АВК: 1 – зуб 1; 2 – зуб 2; 3 – периодонт 1 и 2 зубов; 4 – тело протеза; 5 – сегмент альвеолярного отростка челюсти.
Коронка отсутствующего зуба моделировалась в соответствии с усредненными морфометрическими параметрами второго премоляра, при условии отсутствия в данной области зубочелюстных деформаций.
При расчетах использовались условия закрепления, максимально приближенные к условиям фиксации естественного зуба в окружающих тканях. Для этого моделировался слой периодонта вокруг корня зуба. Предполагалось, что внешняя граница периодонта жестко прикреплена к костной ткани, которая считалась неподвижной. Принято допущение, что толщина периодонта равномерна и составляет 0,3 мм, а ширина альвеолярного отростка в проекции вершин корней зубов достигает 12,4±0,4 мм.
На втором этапе исследования, на основе построенных геометрических моделей АВК, были разработаны четыре конечно-элементные модели. Для обеспечения возможности проведения сравнительного анализа НДС рассматриваемой биомеханической системы при разработке как геометрических, так и конечно-элементных моделей АВК выдвигалось требование идентичности их геометрии и схемы разбиения конечно-элементной сетки. Таким образом, исключалось влияние этих факторов на расчетные значения механических напряжений, возникающих в наиболее нагруженных зонах моделей. В результате все разработанные конечно-элементные модели АВК имели одинаковые количественные характеристики: 245933 элемента, 411141 узел, а также размер, занимаемый на жестком диске – 224 Мбайта (рис. 2).
Приведено описание рассматриваемых моделей биомеханической системы АВК.
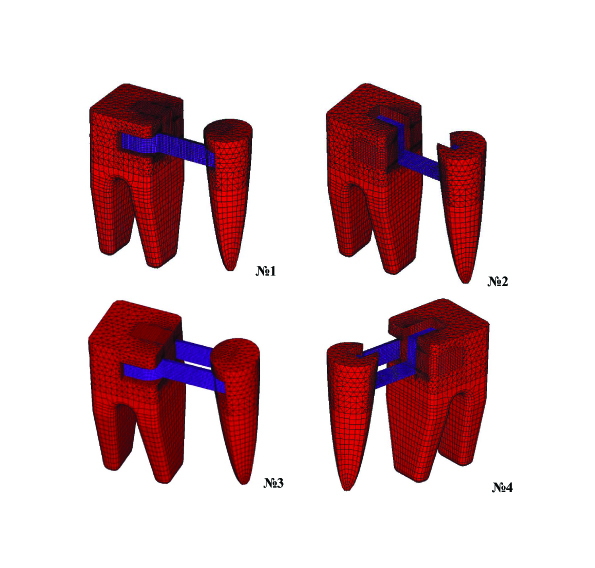
Модель №1: адгезивная волоконная конструкция в системе «зуб-протез» с одним армирующим элементом, который расположен в вертикальной плоскости (перпендикулярно по отношению к альвеолярному отростку челюсти) в межзубном пространстве (теле протеза) и закреплен в той же плоскости на твердых тканях опорных зубов.
Модель №2: адгезивная волоконная конструкция в системе «зуб-протез» с одним армирующим элементом, который расположен в горизонтальной плоскости (параллельно по отношению к альвеолярному отростку челюсти) в межзубном пространстве (теле протеза) и закреплен в той же плоскости на твердых тканях опорных зубов.
Модель №3: адгезивная волоконная конструкция в системе «зуб-протез» с двумя армирующими элементами, которые расположены в вертикальной плоскости (перпендикулярно по отношению к альвеолярному отростку челюсти) в межзубном пространстве (теле протеза) и закреплены в той же плоскости на твердых тканях опорных зубов. При этом элементы каркаса между собой не контактируют, проходя параллельно друг другу.
Модель №4: адгезивная волоконная конструкция в системе «зуб-протез» с двумя армирующими элементами, один из которых расположен в вертикальной (перпендикулярно по отношению к альвеолярному отростку челюсти), а второй – в горизонтальной (параллельно по отношению к альвеолярному отростку челюсти) плоскостях (взаимно перпендикулярно) в межзубном пространстве (теле протеза) и закреплены в тех же плоскостях на твердых тканях опорных зубов.
На рисунке 3 приведены фрагменты конечно-элементных моделей (показаны только опорные зубы и варианты расположения армирующего волокна).
При исследованиях были использованы характеристики следующих составляющих комплексной биомеханической системы «зуб-протез»: дентина и периодонта зубов, альвеолярной кости, композиционного материала FiltekТМ Z-250 (3M ESPE), армирующего волокна Ribbond (Ribbond) (табл. № 1).
В зависимости от принадлежности к той или иной пространственной области модели рассматриваемой биомеханической системы, конечным элементам присваивались соответствующие механические свойства. Затем проводилось описание внешних воздействий и граничных условий. НДС всех элементов адгезивной волоконной конструкции при прочих равных условиях зависит от характера и места приложения нагрузки. С учетом этого факта нагрузка прилагалась к верхней центральной части волоконной конструкции, так как только в этом случае достигается максимальное напряжение между зубом и протезом.
Таблица 1. Механические характеристики материалов
| Материал Параметры |
Волокно Ribbond | Композит FiltekТМ Z-250 | Дентин | Периодонт | Костная ткань |
| Модуль упругости, МПа | 1,7(1075 | 1,77(1044 | 1,83(1044 | 1,18 | 4,9(10² |
| Коэффициент Пуассона, ( | 0,3 | 0,25 | 0,3 | 0,45 | 0,4 |
Нагрузка принята по данным Rus равной 150 Н, т.е. нижнему пределу силы возникающей во время пережевывания твердой пищи в области второго премоляра. Необходимо также отметить, что численное значение нагрузки в данной работе имеет достаточно формальное значение, так как выполняется сравнительный анализ различных вариантов армирования. Рассматривалось два вида нагружения моделей АВК, отличающихся количеством и направлением действующих на центральную часть протеза сил. Первый заключался в приложении к промежуточной части конструкции (телу протеза) только вертикальной силы величиной F1=150 Н, второй – комбинированное действие вертикальной F1 и горизонтальной F2 (в вестибуло-оральном направлении) силы одновременно при величине каждой 150 Н. Нагрузки, действующие на протез, моделировались сосредоточенными силами. Далее для всех четырех моделей выполнялся численный расчет напряженно-деформированного состояния. Данный этап работы благодаря применению программного комплекса конечно-элементного анализа «ANSYS» полностью автоматизирован.
Результаты исследования
Анализ графических и численных данных, полученных в результате проведенного исследования НДС АВК, показал, что для всех рассматриваемых расчетных случаев наибольшие растягивающие и эквивалентные напряжения возникали в композиционном материале конструкций в зоне приложения нагрузки, локализующейся в центре окклюзионной поверхности промежуточной части протеза. Данный факт обусловлен локальным характером приложение нагрузки. Помимо этого, концентрация напряжений в зоне приложения действующих сил не отражает рассматриваемые свойства биомеханической системы АВК. Растягивающие и эквивалентные напряжения для всех 4-х моделей в этой зоне были одинаковы и составили 38,2 МПа и 132 МПа соответственно (растягивающие/эквивалентные) при первом варианте нагружения и 454 МПа и 453 МПа (растягивающие/эквивалентные) при втором. Поэтому зона приложения нагрузки из дальнейшего рассмотрения исключалась.
Следующая по величине развивающихся во всех конструкциях растягивающих и эквивалентных напряжений зона располагалась также в композиционном материале конструкций, в крайней нижней (пришеечной) точке области соединения промежуточной части протеза и моляра. Эта зона показана на примере модели №4 на рисунках 4 и 5 для случаев действия вертикальной и комбинированной нагрузки соответственно.
Полученные в результате проведенного исследования максимальные значения растягивающих и эквивалентных (по Мизесу) напряжений, возникающих в композиционном материале конструкций моделей АВК под действием двух видов нагрузок, представлены в таблице 2.
Таблица 2. Значения максимальных напряжений в материале конструкций (МПа)
| № Модели | Вертикальная нагрузка | Комбинированная нагрузка | ||
| Максимальное растягивающее напряжение | Максимальное эквивалентное напряжение | Максимальное растягивающее напряжение | Максимальное эквивалентное напряжение | |
| 1 | 16 | 15,1 | 45,4 | 42,8 |
| 2 | 12,8 | 12,1 | 52,2 | 49,2 |
| 3 | 13,5 | 12,7 | 42,6 | 40,1 |
| 4 | 12,6 | 11,9 | 41,7 | 39,4 |
Анализ полученных результатов расчета НДС рассматриваемой биомеханической системы АВК показывает, что наименьшие значения механических напряжений в материале конструкции имеют место для модели №4, которой соответствует вариант расположения двух отрезков армирующего волокна во взаимно перпендикулярных областях (рис. 3, модель №4). При действии вертикальной нагрузки максимальные напряжения возникают в композиционном материале конструкции, в крайней нижней (пришеечной) точке области соединения промежуточной части протеза и моляра. В случае действия комбинированной нагрузки зоны возникновения максимальных напряжений не изменяются.
Для более удобного представления и сопоставления полученных данных расчета НДС биомеханической системы АВК, представленных в таблице 2, проведем их сравнительный анализ. Задача этого анализа – определить численные значения, позволяющие отразить преимущество применения варианта расположения армирующего волокна, соответствующего модели №4. С этой целью предложено использовать удельный показатель, характеризующий относительное снижение величины механических напряжений в рассматриваемой биомеханической системе АВК – ∆σ вызванное применением армирующего каркаса модели №4, по сравнению с остальными вариантами. Данный показатель рассчитывался с использованием следующей зависимости:
- где σс – максимальные напряжения в материале конструкции сравниваемого варианта расположения армирующего волокна (модели №1-3) с моделью №4; σб – максимальные напряжения в материале конструкции модели №4.
Полученные в результате расчета удельные показатели представлены в таблице 3.
Таблица 3. Относительное снижение нагруженности материала конструкции
| № модели | Вертикальная нагрузка | Комбинированная нагрузка | ||
| растягивающие напряжения | эквивалентные напряжения | растягивающие напряжения | эквивалентные напряжения | |
| 1 | 21,2 | 21,2 | 8,1 | 7,9 |
| 2 | 1,5 | 1,6 | 20,1 | 19,9 |
| 3 | 6,7 | 6,3 | 2,1 | 1,7 |
Результаты сравнительного анализа нагруженности АВК показывают, что применение варианта расположения двух отрезков армирующего волокна во взаимно перпендикулярных областях, соответствующего модели №4, позволяет снизить механические напряжения в наиболее нагруженных зонах материала конструкции на 20% по сравнению с применением для укладки одного волокна с различной его пространственной ориентацией и на 6,3% по сравнению с применением для армирования двух отрезков волокна, расположенных в вертикальной плоскости. Необходимо отметить, что полученные результаты соответствуют двум наиболее часто встречающимся в клинической практике случаям нагружения АВК – действию только вертикальной, а также комбинированной (вертикальной и горизонтальной) нагрузок. При этом следует отметить, что вариант расположения двух армирующих волокон во взаимно перпендикулярных плоскостях является наиболее эффективным, так как ориентация волокон в нем способствует снижению нагруженности материала конструкций при действии, как одиночной нагрузки, так и сил приложенных в двух взаимно перпендикулярных направлениях.
Выводы
- Расположение двух армирующих волокон во взаимно перпендикулярных плоскостях при действии, как вертикальной, так и комбинированной нагрузки, позволяет снизить механические напряжения в наиболее нагруженных зонах материала АВК до 20% по сравнению с применением одного волоконного каркаса с различной его пространственной ориентацией и до 6,3% по сравнению с применением двух отрезков волокна, расположенных в вертикальной плоскости.
- Концентрация максимальных значений растягивающих и эквивалентных напряжений во всех конструкциях происходит в крайней нижней (пришеечной) точке области соединения промежуточной части протеза и первого моляра.
- При действии изолированной вертикальной нагрузки наибольшие значения растягивающих и эквивалентных напряжений фиксируются в конструкциях с вертикальным вариантом расположения как одного, так и двух армирующих волокон.
- При действии комбинированной нагрузки наибольшие значения растягивающих и эквивалентных напряжений определяются в конструкциях с различными вариантами расположения одного армирующего волокна.
- При изменении направления действующих на АВК сил фиксируется увеличение значений узловых растягивающих и эквивалентных (по Мизесу) напряжений во всех видах конструкций.
Луцкая Ирина Константиновна, д. м. н., профессор, заведующая кафедрой терапевтической стоматологии БелМАПО, Беларусь, Минск
Lutskaya I.K., dms, professor, Head of the Department of Therapeutic Dentistry Belorussian Medical Academy of Postgraduate Education, Belarus, Minsk
Юдина Наталья Александровна, д. м. н., профессор, заведующая кафедрой общей стоматологии Белорусской медицинской академии последипломного образования, Республика Беларусь, Минск
Yudina N. A., Doctor of Medicine, Professor, Head of the Department of General Dentistry, Belarusian Medical Academy of Postgraduate Education, Republic of Belarus, Minsk
г. Минск, ул. П. Бровки 3, кор. 3
Тел: +(375) 17-334-72-86
e-mail: [email protected]
Mathematical analysis of computer modeling of adhesive structures
Аннотация. В статье рассматриваются результаты анализа напряженно-деформированного состояния адгезивных волоконных конструкций, полученного с применением метода конечных элементов. Разработаны компьютерные модели зубных протезов с различными вариантами расположения армирующего каркаса. Проанализировано влияние расположения волокна на возникновение и распределение максимальных значений растягивающих и эквивалентных (по Мизесу) напряжений в конструкции протеза. Установлено, что расположение двух армирующих волокон во взаимно перпендикулярных плоскостях при действии, как вертикальной, так и комбинированной нагрузки, позволяет снизить механические напряжения в наиболее нагруженных зонах материала АВК до 20% по сравнению с применением одного волоконного каркаса с различной его пространственной ориентацией и до 6,3% по сравнению с применением двух отрезков волокна, расположенных в вертикальной плоскости. Проведенный анализ позволил определить и обосновать рациональное расположение волоконного армирующего каркаса адгезивной конструкции, обеспечивающее снижение напряжений.
Annotation. Stress analysis results of dental prosthesis fiber adhesive structures with the use of final element method is discussed in the article. Computer models of dental prosthesis with different reinforcing frame layouts were developed. Reinforcing fiber positioning impact on appearance and distribution of tensile and equivalent (von Mises) stresses in prosthesis structure was analyzed. It has been established that the arrangement of two reinforcing fibers in mutually perpendicular planes under the action of both vertical and combined loads makes it possible to reduce the mechanical stresses in the most loaded zones of the AVK material to 20% compared with the use of one fiber frame with its different spatial orientation and up to 6,3% compared to using two lengths of fiber located in a vertical plane. Carried out analysis made possible to find out and substantiate rational reinforcing fiber frame layout for prosthesis adhesive structure providing stress reduction.
Ключевые слова: адгезивная волоконная конструкция; армирующий каркас; напряженно-деформированное состояние; конечно-элементный анализ.
Key words: fiber adhesive structures; reinforcing frame; stress analysis; final element method.
Литература
- Наумович, С. С. Современные возможности и практическое применение математического моделирования в стоматологии / С. С. Наумович, С. А. Наумович // Современная стоматология. — 2011. -№ 1. — С. 38-42.
- Чернявский, Ю. П. Восстановление целостности зубного ряда адгезивным мостовидным протезом / Ю. П. Чернявский, В. П. Кавецкий // Современная стоматология. — 2006. — № 3. — С. 54-55.
- Чумаченко, Е. Н. Математическое моделирование напряженно-деформированного состояния зубных протезов / Е. Н. Чумаченко, С. Д. Арутюнов, И. Ю. Лебеденко. — М.: Молодая гвардия, 2003. — 271 с.
- Jaroslav, M. Finite element modelling and simulations in dentistry: A bibliography 1990-2003 / M. Jaroslav // Comput Methods Biomech Biomed Engin. — 2004. — Vol. 7. — P. 277-303.
- Provatidis, Ñ. G. A bone-remodelling scheme based on principal strains applied to a tooth during translation / C. G. Provatidis // Computer Methods in Biomechanics & Biomedical Engineering. — 2003. — Vol. 6, № 5-6. — P. 347-352.
- Quasi-automatic 3D finite element model generation for individual single-rooted teeth and periodontal ligament / R. Clement [et al.] // Computer Methods and Programs in Biomedicine. — 2004. — Vol. 73. — P. 135-144.
- Quasi-linear viscoelastic behavior of the human periodontal ligament / S. R. Toms [et al.] //
J. Biomech. — 2002. — Vol. 35 (10). — P. 1411-1415. - Three-dimensional finite element modeling from CT images of tooth and its validation /
K. Tajima [et al.] // Dent. Mater. J. — 2009. — Vol. 28. — P. 219-226.